rosemary
Üye
Stuart Kauffman’ın ‘’Evrende Evimizdeyiz’’ kitabının ön sözünde söylediği ilk cümlelerdeki gibi inanılmaz derecede biyolojik ve evrensel karmaşıklıklarla dolu bir dünyada yaşamaktayız. Hayatın ve evrenin tarihine bu perspektiften bakıldığı zaman canlılar, cansızlar ve ‘cansız olduğunu düşündüklerimiz’ doğal seleksiyonun bir eseridir. ‘’Bu durumda bilime göre bizler uzay ve zamanın oluşturduğu soğuk ve uçsuz bucaksız fondaki akıl almaz derecede düşük olasılıklı kazalar oluruz.’’
Kara delikler hakkında yazdığım yazının ikinci kısmında da ana konumuz kara delikler de olsa genel evren hakkında da ara ara ufak yolculuklara çıkacağız. Önceki kısımda Einstein’ın genel görelilik kavramından biraz bahsetmiştim. O dönemlerde Newton’da, Einstein’da evrenin ya genişlediğini ya da büzülüyor olduğunu söyleyemediler. Fakat Newton zaten evrenin ‘’genişlemesinin’’ gözlemsel keşfinden tam olarak iki yüz elli yıl önce yaşamıştı. Einstein görelilik kuramında evrenin genişlemekte olduğunu öne sürse de, kendisi durağan evrenden o kadar emindi ki sırf kendi kuramını Newton’un kuramına denkleştirmek için ve kütleçekimini dengelemek üzere, kuramına yeni bir sabit ekledi. Yani buradan çıkarılacak sonuç şudur ki ne tarihte, ne bilimde, geçmişteki herhangi bir konuda olayları veya kalıntıları ne kadar derin kazarsak kazalım %100 doğrulukta bir gerçekliğe tam olarak sahip olamayacağız. Bilimin temel ilkelerinde de olduğu gibi, bilimin kendisi de hiçbir zaman ‘’mutlak gerçekliği’’ savunmaz. Bilgiler, kanıtlar her zaman için değişime / gelişime açıktır. Şimdi biraz boyutsal olarak kara deliklerin sınıflandırılmasına bakalım.

Yıldızsal veya diğer adıyla ‘’Stellar’’ kara delikler başlangıçta yaklaşık olarak 10 güneş kütlesi kadar (veya daha fazlası) kütleye sahip bir yıldız kalıntısının içe çökmesi döngüsünün sonucu olarak meydana gelirler. Yıldızsal kara delikler genelde Kerr kara delikleri olarak modellenir, çünkü Kerr modelinin yasalarında da olduğu gibi yıldızın asıl döngüsünün korunması ve bu kara deliklerin çok az elektrik yükü taşıması beklenir.

Dev kara delikler yaklaşık olarak birkaç milyon veya birkaç milyar güneş kütlesi arasında değişen bir kütleye sahiptir. Bilim insanları tarafından yalnızca azımsanamayacak kadar az dev kara delik bulundu. Fakat elbette evrende bu dev kara deliklerden belki de milyarlarca olduğu tahmin ediliyor. Gök bilimciler kara deliğe yakın yıldızların hızını ölçerek kütlesini tahmin edebilirler. Örnek verecek olursak Nasa çalışmalarına göre galaksimizin merkezindeki kara deliğin, Güneş’in yaklaşık dört milyon katı kadar bir kütleye sahip olduğunu bu şekilde bilebiliyorlar.

Leo I (Dwarf Galaxy)
Bu görseldeki galaksi her ne kadar toplamda sadece 20 milyon güneş kütlesi kadar olsa da, merkez kara deliği de doğru orantılı olarak o kadar büyük, yani yaklaşık 3 milyon güneş kütlesinde.
Orta kara delikler

Yakın zamanda keşfedilmiş olan bu kara delikler 100 ila 10.000 güneş kütlesi arasında değişen bir büyüklüğe sahiptirler. Orta kütleli kara deliklerin en güncel örneği Sloan Dijital Gökyüzü Araştırması (SDSS) tarafından toplanan bir milyon gökada optik spektrumunun karmaşık birtakım analiziyle seçilen 305 gökadayı içermektedir. Fakat henüz orta kara deliklerle alakalı çok geniş kapsamlı araştırmalar yapılamadı.
İlksel kara delikler

Mikro veya kuantum kara delikleri olarak da bilinen bu kara delikler çok küçük boyutlara sahiptirler. ‘’İlksel’’ adının verilme nedeni ise Büyük Patlama sırasında oluştuklarının düşünülmesindendir. Stephen Hawking ve Bernard Carr yaptıkları çeşitli kozmos çalışmalarında kara delik kavramını geliştirerek ‘’mini kara delik’’ adını verdikleri bu oluşumların evrende bol miktarda bulunduğunu öne sürdüler. Bu kara deliklerin yoğunlukları hakkında henüz kesin bir bilgi bulunmamaktadır.
*Bu alanda çalışan bazı fizikçilere göre ilksel kara deliklerin daha küçük benzer örnekleri LHC (Large Hadron Collider) yani Büyük Hadron Çarpıştırıcısı gibi ‘’parçacık hızlandırıcı’’ kullanılarak laboratuvarda da oluşturulabilir.
Kara deliklerin Entropisi
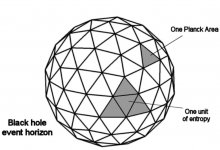
Bekenstein- Hawking entropisi veya kara delik entropisi, bir kara deliğin dışındaki gözlemciler tarafından yorumlandığı haliyle termodinamik yasalarına uyması için bir kara deliğe atanması gereken entropi miktarıdır. Kara delik entropisi geometrik kökenlidir fakat artı olarak birçok fiziksel sonucu da olan bir kavramdır. Bekenstein - Hawking entropisi; yerçekimi, termodinamik ve kuantum teorisinden türeyen kavramların kesişim noktasıdır ve bu nedenle kuantum tabanlı yerçekiminin henüz açıklanamayan gizli ve tozlu dünyasına açılan bir pencere olarak kabul edilir. 1971’de Stephen Hawking, bütün kara delik türlerinde ‘’olay ufku’’ yüzeyinin hiçbir zaman küçülmediğini ortaya koydu. Bu özellik, entropi (çözülüm, dağılım, yok oluş) rolünü üstlenen yüzey bakımından tam olarak ‘’termodinamiğin ikinci yasası’’nı* andırır. Bilinen ve klasik fizik baz alındığında termodinamiğin bu yasası bir kara deliğe madde gönderildikten sonra onun kozmosumuzda yok olmasını sağlayarak ihlal edilebilir. Kara deliklerin entropisinin keşfi, kara delikler ile termodinamiğin arasında son derece bir benzeşim ilişkilerinin kurulmasına yol açmıştır. Böylece ‘’kuantum çekimi’’** konusunun da daha anlaşılabilir kılınmasına kolaylık sağlamıştır.
Kara deliklerle ilgili henüz çok fazla bilgiye erişememiş veya açıklığa kavuşturamamış olsak da, açıklığa kavuşturulan konular da bir o kadar uzun. Henüz değinmediğim bir sürü konu var. Örneğin, ‘’Hawking Işınımı’’, ‘’Ergosfer Alanı’’, ‘’Foton Küresi’’, ‘’Gravitasyonel Dalgalar’’ ve daha nicesi… Fakat bu saydıklarım ve bundan sonrakiler çok fazla formül + matematik / fizik bilgisi istediğinden, formülleri bilmeyen okuyucular için biraz sıkıcı olabilir, ki bu formülleri basite indirgeyerek veya cümleler halinde anlatmak da oldukça zor. O yüzden kara deliklerle ilgili açıklamak istediğim son konuya gelmiş bulunuyoruz.
* Termodinamiğin ikinci yasası: izole sistemlerin entropisinin asla azalamayacağını belirtir. Bunun sebebini izole sistemlerin termodinamik dengeden (maksimum entropi aşaması) spontane olarak oluşmasıyla açıklar. Zamana bağlı bir ifade olarak; sıcaklık, basınç ve kimyasal potansiyel ısıbilgisi dengeye doğru izole edilmiş ve yerçekiminin önemsiz olduğu sistemde azalır. İkinci yasa farklı birçok şekilde açıklanabilir ama ilk formülasyon 1824 yılında Fransız bilim insanı Sadi Carnot tarafından yazılmıştır.
** Kuantum Çekimi: Kuantum Kütleçekimi, kuramsal fiziğin bir dalı olup doğanın temel kuvvetlerinden üçünü (elektromanyetizm ve etkileşimleri) tanımlayan, kuantum mekaniği dördüncü temel kuvveti kütleçekiminin kuramı olan, genel göreliliği birleştireceği düşünülen bir kuramdır.
Enformasyon Paradoksu
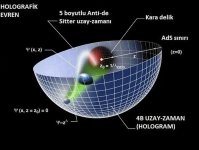
Bu konu olay ufkundan daha gizemli bir konudur. 21. Yüzyıl başından beri hala çözülemeyen temel fizik meselelerinden biridir. ‘’Saçsızlık Kuramı’’* sebebiyle kara deliklerin içine girmiş olan herhangi bir şeyi saptamak mümkün değildir. Fakat kara delikten uzak olan bir gözlemci tarafından düşünürsek, bu enformasyon tümüyle yok olmuş sayılmaz. Şöyle ki, önceden kara deliğe düşmüş olan bir madde, ışık yılı göz önüne alındığında, bu madde gözlemci tarafından hala görülebilir durumda oluyor. Pekala, o zaman kara deliği oluşturan bu enformasyon kayıp mıdır, değil midir? Bu konuda ‘’Hawking Işınımı’’ değişkeninden ziyade, ufuk entropisi değişkenliği daha tatminkâr bulunmaktadır. Tüm bunlara rağmen Enformasyon Paradoksu’’da ‘henüz gizemi çözülememiş olanlar’ isimli raftaki makamını korumakta.
* Saçsızlık Kuramı: Genel görelilikte Einstein - Maxwell yerçekimi ve elektromanyetizma denklemlerinin tüm sabit kara delik çözümlerinin yalnızca üç bağımsız, dışarıdan gözlemlenebilir klasik parametrelerle açıklanabileceğini belirtir. Bu üç parametre kütle, elektrik yükü ve açısal momentumdur. Buna saçsızlık teoremi adı verilir. Bu ismin verilme sebebini basitçe açıklayacak olursak; saçı olmayan birini ‘’kel’’ diyerek tanımlamak yeterliyken, saçı olan birini tanımlamak için saçının rengi, uzunluğu vs. gibi verilere ihtiyaç vardır. Kara delikler de aynı şekilde çok az veriyle tanımlanabildikleri için bu kurama ‘’saçsızlık kuramı’’ adı verilmiştir.
Son olarak, diğer gezegenler, evrendeki diğer oluşumlar veya yıldızlar gibi kara delikler de son derece insanlarla benzeşen oluşumlardır. Hayatınızdaki kara deliklerin sizi karanlıklarına çekip yutmasına ve hayatınızı zindana çevirmesine asla izin vermeyin.
Kaynakça
Linkler: https://tr.wikipedia.org/wiki/Kara_delik#endnote_57
https://evrimagaci.org/kara-delik-nedir-kara-delik-nasil-olusur-7748
https://en.wikipedia.org/wiki/Supermassive_black_hole
https://www.space.com/supermassive-black-hole
https://astronomy.swin.edu.au/cosmos/s/Stellar+Black+Hole
https://www.nasa.gov/mission_pages/chandra/multimedia/igr.html
https://www.astronomy.com/page/2/?s=supermassive+black+holes
http://www.scholarpedia.org/article/Bekenstein-Hawking_entropy
https://www.mdpi.com/1099-4300/22/1/1
Kitaplar: Immanuel Kant - Evrensel Doğa Tarihi ve Gökler Kuramı
Stephen Hawking - Kara Delikler ve Bebek Evren
Stuart Kauffman - Evrende Evimizdeyiz
[BGCOLOR=rgba(255, 255, 255, 0)]Robert M. Wald, "General Relativity", University of Chicago Press, 1984[/BGCOLOR]
*Bu alanda çalışan bazı fizikçilere göre ilksel kara deliklerin daha küçük benzer örnekleri LHC (Large Hadron Collider) yani Büyük Hadron Çarpıştırıcısı gibi ‘’parçacık hızlandırıcı’’ kullanılarak laboratuvarda da oluşturulabilir.
Kara deliklerin Entropisi

Bekenstein- Hawking entropisi veya kara delik entropisi, bir kara deliğin dışındaki gözlemciler tarafından yorumlandığı haliyle termodinamik yasalarına uyması için bir kara deliğe atanması gereken entropi miktarıdır. Kara delik entropisi geometrik kökenlidir fakat artı olarak birçok fiziksel sonucu da olan bir kavramdır. Bekenstein - Hawking entropisi; yerçekimi, termodinamik ve kuantum teorisinden türeyen kavramların kesişim noktasıdır ve bu nedenle kuantum tabanlı yerçekiminin henüz açıklanamayan gizli ve tozlu dünyasına açılan bir pencere olarak kabul edilir. 1971’de Stephen Hawking, bütün kara delik türlerinde ‘’olay ufku’’ yüzeyinin hiçbir zaman küçülmediğini ortaya koydu. Bu özellik, entropi (çözülüm, dağılım, yok oluş) rolünü üstlenen yüzey bakımından tam olarak ‘’termodinamiğin ikinci yasası’’nı* andırır. Bilinen ve klasik fizik baz alındığında termodinamiğin bu yasası bir kara deliğe madde gönderildikten sonra onun kozmosumuzda yok olmasını sağlayarak ihlal edilebilir. Kara deliklerin entropisinin keşfi, kara delikler ile termodinamiğin arasında son derece bir benzeşim ilişkilerinin kurulmasına yol açmıştır. Böylece ‘’kuantum çekimi’’** konusunun da daha anlaşılabilir kılınmasına kolaylık sağlamıştır.
Kara deliklerle ilgili henüz çok fazla bilgiye erişememiş veya açıklığa kavuşturamamış olsak da, açıklığa kavuşturulan konular da bir o kadar uzun. Henüz değinmediğim bir sürü konu var. Örneğin, ‘’Hawking Işınımı’’, ‘’Ergosfer Alanı’’, ‘’Foton Küresi’’, ‘’Gravitasyonel Dalgalar’’ ve daha nicesi… Fakat bu saydıklarım ve bundan sonrakiler çok fazla formül + matematik / fizik bilgisi istediğinden, formülleri bilmeyen okuyucular için biraz sıkıcı olabilir, ki bu formülleri basite indirgeyerek veya cümleler halinde anlatmak da oldukça zor. O yüzden kara deliklerle ilgili açıklamak istediğim son konuya gelmiş bulunuyoruz.
* Termodinamiğin ikinci yasası: izole sistemlerin entropisinin asla azalamayacağını belirtir. Bunun sebebini izole sistemlerin termodinamik dengeden (maksimum entropi aşaması) spontane olarak oluşmasıyla açıklar. Zamana bağlı bir ifade olarak; sıcaklık, basınç ve kimyasal potansiyel ısıbilgisi dengeye doğru izole edilmiş ve yerçekiminin önemsiz olduğu sistemde azalır. İkinci yasa farklı birçok şekilde açıklanabilir ama ilk formülasyon 1824 yılında Fransız bilim insanı Sadi Carnot tarafından yazılmıştır.
** Kuantum Çekimi: Kuantum Kütleçekimi, kuramsal fiziğin bir dalı olup doğanın temel kuvvetlerinden üçünü (elektromanyetizm ve etkileşimleri) tanımlayan, kuantum mekaniği dördüncü temel kuvveti kütleçekiminin kuramı olan, genel göreliliği birleştireceği düşünülen bir kuramdır.
Enformasyon Paradoksu

Bu konu olay ufkundan daha gizemli bir konudur. 21. Yüzyıl başından beri hala çözülemeyen temel fizik meselelerinden biridir. ‘’Saçsızlık Kuramı’’* sebebiyle kara deliklerin içine girmiş olan herhangi bir şeyi saptamak mümkün değildir. Fakat kara delikten uzak olan bir gözlemci tarafından düşünürsek, bu enformasyon tümüyle yok olmuş sayılmaz. Şöyle ki, önceden kara deliğe düşmüş olan bir madde, ışık yılı göz önüne alındığında, bu madde gözlemci tarafından hala görülebilir durumda oluyor. Pekala, o zaman kara deliği oluşturan bu enformasyon kayıp mıdır, değil midir? Bu konuda ‘’Hawking Işınımı’’ değişkeninden ziyade, ufuk entropisi değişkenliği daha tatminkâr bulunmaktadır. Tüm bunlara rağmen Enformasyon Paradoksu’’da ‘henüz gizemi çözülememiş olanlar’ isimli raftaki makamını korumakta.
* Saçsızlık Kuramı: Genel görelilikte Einstein - Maxwell yerçekimi ve elektromanyetizma denklemlerinin tüm sabit kara delik çözümlerinin yalnızca üç bağımsız, dışarıdan gözlemlenebilir klasik parametrelerle açıklanabileceğini belirtir. Bu üç parametre kütle, elektrik yükü ve açısal momentumdur. Buna saçsızlık teoremi adı verilir. Bu ismin verilme sebebini basitçe açıklayacak olursak; saçı olmayan birini ‘’kel’’ diyerek tanımlamak yeterliyken, saçı olan birini tanımlamak için saçının rengi, uzunluğu vs. gibi verilere ihtiyaç vardır. Kara delikler de aynı şekilde çok az veriyle tanımlanabildikleri için bu kurama ‘’saçsızlık kuramı’’ adı verilmiştir.
Son olarak, diğer gezegenler, evrendeki diğer oluşumlar veya yıldızlar gibi kara delikler de son derece insanlarla benzeşen oluşumlardır. Hayatınızdaki kara deliklerin sizi karanlıklarına çekip yutmasına ve hayatınızı zindana çevirmesine asla izin vermeyin.
Kaynakça
Linkler: https://tr.wikipedia.org/wiki/Kara_delik#endnote_57
https://evrimagaci.org/kara-delik-nedir-kara-delik-nasil-olusur-7748
https://en.wikipedia.org/wiki/Supermassive_black_hole
https://www.space.com/supermassive-black-hole
https://astronomy.swin.edu.au/cosmos/s/Stellar+Black+Hole
https://www.nasa.gov/mission_pages/chandra/multimedia/igr.html
https://www.astronomy.com/page/2/?s=supermassive+black+holes
http://www.scholarpedia.org/article/Bekenstein-Hawking_entropy
https://www.mdpi.com/1099-4300/22/1/1
Kitaplar: Immanuel Kant - Evrensel Doğa Tarihi ve Gökler Kuramı
Stephen Hawking - Kara Delikler ve Bebek Evren
Stuart Kauffman - Evrende Evimizdeyiz
[BGCOLOR=rgba(255, 255, 255, 0)]Robert M. Wald, "General Relativity", University of Chicago Press, 1984[/BGCOLOR]
Son düzenleme:
